If Synthetic Division Reveals a Zero Why Should We Try That Value Again as a Possible Solution

3.6e: Exercises - Zeroes of Polynomial Functions

1. Last updated

2. Save as PDF

Page ID

45013

A:Concepts

Exercise \(\PageIndex{A}\): Concepts

1) Describe a use for the Balance Theorem.

2) Explicate why the Rational Zero Theorem does not guarantee finding zeros of a polynomial office.

3) What is the difference between rational and real zeros?

4) If Descartes' Rule of Signs reveals a \(0\) or \(1\) change of signs, what specific conclusion can exist fatigued?

5) If synthetic division reveals a zero, why should nosotros endeavour that value once more as a possible solution?

Answers to odd exercises:

ane. The theorem can be used to evaluate a polynomial.

three. Rational zeros can be expressed as fractions whereas real zeros include irrational numbers.

5. Polynomials can have repeated zeros, and so the fact that number is a zero doesn't preclude information technology existence a nil once more.

B:Employ the Remainder Theorem to Evaluate a Polynomial

Exercise \(\PageIndex{B}\): Use the Residuum Theorem

\( \bigstar \)Utilize synthetic sectionalization to evaluate \(p(c)\) and write \(p(10)\) in the form \(p(x) = (x-c) q(x) +r\).

half-dozen. \(p(x) = 2x^2 - 10 + 1\), \(c = iv\) 7. \(p(x) = 4x^2-33x-180\), \(c = 12\) 8. \(p(10) = 2x^3 - x + 6\), \(c=-3\) 9. \(p(x) = 10^3+2x^2+3x+4\), \(c =-1\) 10. \(p(x) =3x^3-6x^ii+4x-8\), \(c=ii\)

11. \(p(x) = 8x^3+12x^ii+6x+1\), \(c =-\frac{i}{2}\) 12. \(p(x) = 2x^4 +ten^3- 4x^2+10x-7\), \(c=\frac{3}{2}\) thirteen.  \(p(x) = x^4 - 3x^iii - 20x^ii - 24x - 8\), \(c =7\) xiv. \(p(x) = ten^iv - 5x^ii - 8x -12\), \(c=3\) 15. \(p(x) = 10^4 - 5x^3 + x^2 + 5\), \(c =2\)

Answers to odd exercises:

7. \(p(12) =0\), \(p(10) = (x-12)(4x+15) \) ix. \(p(-i)=2\), \(p(10) = (10+1)(x^2 + x+2) + 2 \) xi. \(p\left(-\frac{1}{2}\right) = 0\), \(p(10) = (2x+1)(4x^two+4x+1)\)

xiii. \(p(seven)=216\), \(p(x) = (x-vii)(x^3+4x^ii +8 x+32) + 216 \) xv. \(p(2)=-fifteen\), \(p(x) = (x-2)(x^three-3x^2 -5x -10) -fifteen \)

C:Given 1 zero or factor, find all Real Zeros, and gene a polynomial

Exercise \(\PageIndex{C}\): Use the Factor Theorem given one cypher or cistron

\( \bigstar \)Given a polynomial and one of its factors, find the rest of the real zeros and write the polynomial as a production of linear and irreducible quadratic factors.

17) \(f(x)=2x^3+x^two−5x+2;\) Factor: \( ( 10+2) \) 18) \(f(x)=3x^3+x^2−20x+12;\) Gene: \( ( x+iii)\) 19) \(f(x)=2x^iii+3x^2+10+6;\) Factor: \( (ten+2)\) 20) \(f(x)=−5x^three+16x^ii−9;\) Gene: \( (x−3)\)

21) \(f(x)=x^3+3x^2+4x+12;\) Factor: \( (x+three)\) 22) \(f(ten)=4x^3−7x+3;\) Factor: \( (x−1)\) 23) \(f(x)=2x^3+5x^2−12x−30;\) Factor: \( (2x+5)\) 24) \(f(x)=2x^3−9x^2+13x−6;\) Cistron: \( (ten−1) \)

Answers to odd exercises:

17. \(−2, one, \frac{1}{two}\); \( f(ten)=(x+2)(10-1)(2x-1) \) xix. \(−2\); \( f(x)=(x+two)(2x^2-x+three) \)

21. \(−3\); \( f(10)=(x+3)(ten^two+4) \) 23. \(−\frac{five}{2},\; \sqrt{six},\; −\sqrt{6}; \) \(f(x)=(2x+5)(ten-\sqrt{6})(x+\sqrt{6})\)

\( \bigstar \)Given a polynomial and \(c\), one of its zeros, find the rest of the real zeros and write the polynomial as a production of linear and irreducible quadratic factors. Information technology is possible some factors are repeated.

25. \(p(x)=x^{iii} - 24x^{2} + 192x - 512, \;\; c = 8\) 26. \(p(x)=3x^{3} + 4x^{two} - ten - 2, \;\; c = \frac{2}{3}\) 27. \(p(x)=2x^3-3x^2-11x+6, \;\; c=\frac{1}{2}\) 28. \(p(10)=x^iii+2x^ii-3x-6, \;\; c = -2\) 29. \(p(x)=2x^3-x^2-10x+v, \;\; c=\frac{1}{2}\)

xxx. \(p(ten)=4x^{4} - 28x^{iii} + 61x^{2} - 42x + nine,\; c = \frac{one}{2}\) 31. \(p(ten)=x^v+2x^4-12x^iii-38x^2-37x-12,\) \(\; c=-ane\) 32. \(p(x)=2x^5 +7x^4 - 18x^2 - 8x +eight,\)  \(\; c = \frac{1}{ii}\) 33. \(p(10)=3x^5 +2x^4 - 15x^3 -10x^2 +12x +eight,\)  \(\; c = -\frac{2}{3}\)

Answers to odd exercises:

25. zeros: \(8\);  \(p(ten)= (10 - 8)^{3}\) 27. zeros: \( \frac{1}{2}, -2, 3 \);  \(p(10)= (2x-one)(x+2)(x-three)\) 29. zeros: \( \frac{1}{ii}, \pm \sqrt{5} \);  \(p(x)= (2x-one)(ten+\sqrt{5})(x-\sqrt{v})\)

31. zeros: \( -i,\) \(-3,\) \(4\);  \(p(ten)= (x+1)^iii(x+three)(ten-4)\) 33. zeros: \( -2,\; -1,\; -\frac{two}{3},\; 1,\; two \\ \); \( \quad\)  \(p(10)= (x+2)(x+1)(ten-i)(x-ii)(3x+two)\)

D: List all Possible Rational Zeros

Practice \(\PageIndex{D}\): Use the Rational Zero Theorem

\( \bigstar \)Employ the Rational Zeros Theorem to list all possible rational zeros for each given role.

35) \(f(x)=2x^3+3x^two−8x+5\) 36) \(f(ten)=3x^3+5x^two−5x+iv\) 37) \(f(x)=6x^four−10x^two+13x+one\) 38) \(f(10)=4x^5−10x^4+8x^three+x^2−8\)

39. \(f(x) = x^{3} - 2x^{2} - 5x + 6\) 40. \(f(x) = 10^{iv} + 2x^{3} - 12x^{2} - 40x - 32\) 41. \(f(x) = x^{three} - 7x^{2} + x - 7\) 42. \(f(10) = ten^{3} + 4x^{two} - 11x + six\) 43. \(f(x) = x^{4} - 9x^{two} - 4x + 12\)

44. \(f(10) = -2x^{3} + 19x^{2} - 49x + 20\) 45. \(f(x) = -17x^{3} + 5x^{2} + 34x - 10\) 46. \(f(x) = 36x^{4} - 12x^{iii} - 11x^{ii} + 2x + one\) 47. \(f(ten) = 3x^{three} + 3x^{2} - 11x - 10\) 48. \(f(x) = 2x^four+x^3-7x^ii-3x+iii\)

Answers to odd exercises:

35. \(±v, ±1, ± \frac{1}{2}, ± \frac{five}{2}\) 37. \(±1, ±\frac{ane}{ii}, ±\frac{1}{3}, ±\frac{1}{half dozen}\) 39. \(\pm 1\), \(\pm 2\), \(\pm iii\), \(\pm vi\) \(\qquad \qquad\) 41. \(\pm 1\), \(\pm vii\)

43. \(\pm 1\), \(\pm 2\), \(\pm iii\), \(\pm 4\), \(\pm 6\), \(\pm 12\) 45. \(\pm 1\), \(\pm 2\), \(\pm v\), \(\pm 10\), \(\pm \frac{ane}{17}\),\(\pm \frac{2}{17}\),\(\pm \frac{5}{17}\),\(\pm \frac{10}{17}\) 47. \(\pm 1\), \(\pm two\), \(\pm 5\), \(\pm x\), \(\pm \frac{one}{iii}\),\(\pm \frac{two}{3}\),\(\pm \frac{five}{3}\),\(\pm \frac{ten}{three}\)

E:Find all Zeros that are Rational

Exercise \(\PageIndex{Eastward}\): Find all zeros that are rational

\( \bigstar \)Use the Rational Zero Theorem to discover all existent number zeros.

49) \(x^3−3x^2−10x+24=0\) 50) \(2x^three+7x^2−10x−24=0\) 51) \(x^3+2x^two−9x−xviii=0\) 52) \(10^3+5x^2−16x−80=0\) 53) \(x^3−3x^2−25x+75=0\)

54) \(2x^3−3x^2−32x−fifteen=0\) 55) \(2x^3+x^2−7x−6=0\) 56) \(2x^3−3x^2−x+1=0\) 57) \(3x^3−10^2−11x−half dozen=0\) 58) \(x^four−2x^3−7x^ii+8x+12=0\)

59) \(4x^3−3x+ane=0\) 60) \(4x^4+4x^3−25x^two−10+6=0\) 61) \(x^four+2x^three−9x^2−2x+8=0\) 62) \(10^4+2x^3−4x^2−10x−v=0\) 63) \(-5x^iv+4x^three−19x^2+16x+four=0\)

Answers to odd exercises:

49. \(-3,\; 2,\; 4\) 51. \(-ii,\; 3,\; −three\)

53. \(three, −5, 5 \) 55. \(2,\; -1,\; -\frac{3}{ii}\)

57. \( -\frac{2}{iii} ,\; \frac{one \pm \sqrt{13}}{2} \) 59. \( -1,\; \frac{1}{ii} \)

61. \(one,\; ii,\; −1,\; −4\) 63. \(−\frac{1}{five},\; 1  \)

\( \bigstar \)Detect the real zeros of the polynomial. State the multiplicity of each existent zero.

65. \(f(ten) = ten^{three} - 2x^{2} - 5x + 6\) 66. \(f(x) = ten^{3} + 4x^{2} - 11x + half-dozen\)

67. \(f(ten) = x^{4} - 9x^{2} - 4x + 12\) 68. \(f(x) = -17x^{3} + 5x^{ii} + 34x - ten\) 69. \(f(x) = 36x^{4} - 12x^{three} - 11x^{ii} + 2x + 1\)

70. \(f(ten) = 2x^4+10^3-7x^2-3x+iii\) 71. \(f(ten) = 2x^{3} + 7x^{two} +4x - 4\) 72. \(f(x) = -2x^4 - 3x^3 +10x^2 + 12x - viii\)

Answers to odd exercises:

65. \(x = ane\) (mult. 1), \(x = three\) (mult. i), \(x = -two\) (mult. 1) 67. \(x = -2\) (mult. 2), \(x = 1\) (mult. ane), \(x = 3\) (mult. 1)

69. \(10 = \frac{1}{2}\) (mult. two), \( ten = -\frac{i}{3}\) (mult. 2) 71.  \(10 = -2\) (mult. 2), \(10 = \frac{one}{2}\) (mult. 1)

F:Find all zeros (both real and imaginary)

Exercise \(\PageIndex{F}\): Discover all zeros

\( \bigstar \)Employ the Rational Zero Theorem to find all complex solutions (existent and not-real).

72) \(ten^3+ten^2+x+1=0\) 73) \(x^three−8x^two+25x−26=0\)

74) \(10^3+13x^2+57x+85=0\) 75) \(3x^3−4x^2+11x+10=0\)

76) \(x^four+2x^iii+22x^two+50x−75=0\) 77) \(2x^3−3x^two+32x+17=0\)

Answers to odd exercises:

73. \(2, 3+2i, 3−2i\)

75. \(−\dfrac{2}{3}, one+2i, 1−2i\)

77. \(−\dfrac{1}{2}, i+4i, ane−4i\)

G:Find all zeros and sketch

Practise \(\PageIndex{One thousand}\): Discover all zeros and sketch

\( \bigstar \)Determine the end behaviour, all the real zeros, their multiplicity, and y-intercept. Sketch the function. (Apply synthetic division to find a rational zero. Employ the quotient to notice the next goose egg).

78) \(f(x)=x^iii−1\) 79) \(f(10)=x^iv−x^two−1\) 80) \(f(x)=ten^3−2x^two−5x+6\) 81) \(f(10)=2x^3+37x^2+200x+300\) 82) \(f(x)=x^4+2x^3−12x^2+14x−v\)

83) \(f(x)=2x^4−5x^three−5x^two+5x+3\) 84) \(f(x)=10^3−2x^2−16x+32\) 85) \(f(x)=-ten^3−7x^two-8x+16\) 86. \(f(10) = -x^four - 4x^3+3x^2 +10x -8\)

87. \(f(x) =  10^{4} - 6x^{3} + 8x^{ii} + 6x - 9\) 88. \(f(x) = x^{4} + 4x^{3} - 5x^{two} - 36x - 36\) 89. \(f(x) = x^{5} - 10^{4} - 5x^{iii} + x^{2} + 8x + 4\) 90. \(f(10) = x^{four} + 2x^{3} + 6x - 9\)

Answers to odd exercises:

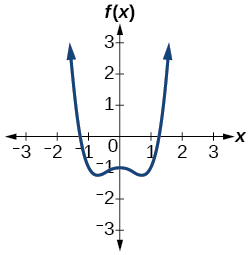
79. zeros (odd multiplicity): \( \pm \sqrt{ \frac{1+\sqrt{five} }{2} }\), ii imaginary zeros, y-intercept \( (0, 1) \)	81. zeros (odd multiplicity): \( \{-10, -6,  \frac{-5}{2} \} \); y-intercept: \( (0, 300) \)	83. zeros (odd multiplicity); \( \{ -1, 1, 3, \frac{-1}{2} \} \), y-intercept \( (0,3) \).
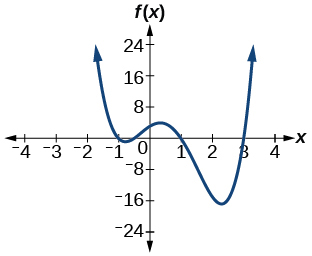
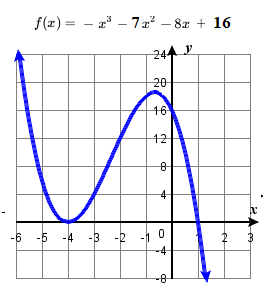
85. zeros; \(-4\) (multiplicity \(two\)), \(one\) (multiplicity \(1\)), y-intercept \( (0,xvi) \).	87.  odd multiplicity zeros: \( \{ane, -i\} \); even multiplicity zero: \( \{ three \} \); y-intercept \( (0, -ix) \).	89. odd multiplicity nada: \( \{ -1 \} \), even multiplicity zero \( \{ 2 \} \). y-intercept \( (0, 4) \).

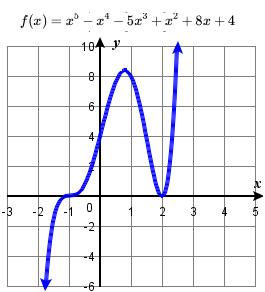
H:Given zeros, construct a polynomial role

Exercise \(\PageIndex{H}\): Given zeros, construct a polynomial function

\( \bigstar \)Construct a polynomial office of least degree possible using the given information. You may leave the polynomial in factored form.

91) A lowest degree polynomial with real coefficients and zero \( 3i \)

92) A lowest caste polynomial with rational coefficients and zeros: \( two \) and \( \sqrt{6} \)

93) A lowest degree polynomial with integer coefficients and Real roots: \(–1\) (with multiplicity \(2\)), and \(ane\).

94) A lowest degree polynomial with integer coefficients and Real roots: \(–two\), and \(\frac{one}{2}\) (with multiplicity \(ii\))

95) A lowest degree polynomial with integer coefficients and Real roots:\(−\frac{1}{two}, 0,\frac{one}{2}\)

96) A everyman caste polynomial with integer coefficients and Real roots: \(–4, –1, ane, 4\)

97) A lowest degree polynomial with integer coefficients and Real roots: \(–1, 1, 3\)

98. A lowest degree polynomial with real coefficients and zeros: \(-2 \) and \( -5i \)

99. A everyman degree polynomial with real coefficients and zeros: \(4 \) and \( 2i \).

100. The solutions to \(p(x) = 0\) are \(10 = \pm iii\) and \(10=6\).  The leading term of \(p(x)\) is \(7x^4\).
\(\qquad\)The indicate \((-3,0)\) is a local minimum on the graph of \(y=p(x)\).

101. The solutions to \(p(x) =0\) are \(x = \pm three\), \(ten=-2\), and \(x=iv\), The leading term of \(p(x)\) is \(-x^5\).
\(\qquad\)The point \((-2, 0)\) is a local maximum on the graph of \(y=p(x)\).

102. \(p\) is caste 4. as \(x \rightarrow \infty\), \(p(10) \rightarrow -\infty\) \(p\) has exactly three \(x\)-intercepts: \((-6,0)\), \((1,0)\) and \((117,0)\).
\(\qquad\)The graph of \(y=p(10)\) crosses through the \(10\)-axis at \((one,0)\).

103. Detect a quadratic polynomial with integer coefficients which has \(10 = \dfrac{3}{five} \pm \dfrac{\sqrt{29}}{5}\) equally its real zeros.

Answers to odd exercises:

91. \(f(ten)=(x^2+9)\) 93. \(f(x)=(x+i)^2(x-ane)\) 95. \(f(x)=x(2x+i)(2x-1)\) 97. \( f(x) = (x+1)(x-one)(ten-iii) \)

99. \(p(x)= (x-four)(10-2i)(x+2i)=x^3-4x^2+4x-16\) 101. \(p(x) = -(x + ii)^{two}(10 - three)(10 + 3)(x - four)\) 103. \(p(x) = 5x^{2} - 6x - four\)

I: UseIntermediate Value Theorem

Exercise \(\PageIndex{I}\): Intermediate Value Theorem

\( \bigstar \)Apply the Intermediate Value Theorem to confirm the polynomial \(f\) has at least one zero within the given interval.

104) \(f(x)=x^iii−9x\), between \(x=−4\) and \(x=−two\). 105) \(f(10)=x^3−9x\), between \(x=2\) and \(x=iv\). 106) \(f(ten)=ten^5−2x\), betwixt \(x=1\) and \(10=2\).

107) \(f(x)=−x^4+4\), between \(ten=i\) and \(10=3\). 108) \(f(x)=−2x^3−x\), betwixt \(x=–1\) and \(x=1\). 109) \(f(10)=ten^3−100x+ii\), between \(x=0.01\) and \(ten=0.1\)

Answers to odd exercises:

105. \(f(2)=–x,\; f(four)=28\). \(\qquad\)Sign change confirms.

107. \(f(1)=3,\; f(3)=–77.\) \(\qquad\)Sign change confirms.

109. \(f(0.01)=ane.000001,\; f(0.1)=–7.999\). \(\qquad\)Sign change confirms.

x

greenfrid1950.blogspot.com

Source: https://math.libretexts.org/Courses/Monroe_Community_College/MTH_165_College_Algebra_MTH_175_Precalculus/03:_Polynomial_and_Rational_Functions/3.06:_Zeros_of_Polynomial_Functions/3.6E:_Exercises_-_Zeroes_of_Polynomial_Functions

Share this post